Mutable and immutable operations
Immutable operations do not modify the passed in frames but always return a new one. Given an input frame, an immutable function will always return the same result. Immutable operations are performed using such functions as AUG(), FILTER(), GROUP_BY(), as well as the pipe operator.
Mutable operations, on the other hand, modify the passed in frame in place. Mutable operations are performed using such functions as ADD_COLUMN(), ADD_ROW(), DELETE_ROW(), SET_FRAME_CELL(), etc.
To better understand the difference between the immutable and mutable operations, let's take the data in the range A1:A4 below and create a frame from the data.
| A | B | |
|---|---|---|
| 1 | product | |
| 2 | apples | |
| 3 | bananas | |
| 4 | kiwi | |
| 5 | ||
| 6 | =FRAME(A1:A4) |
As a result, we have the following frame in cell A6:
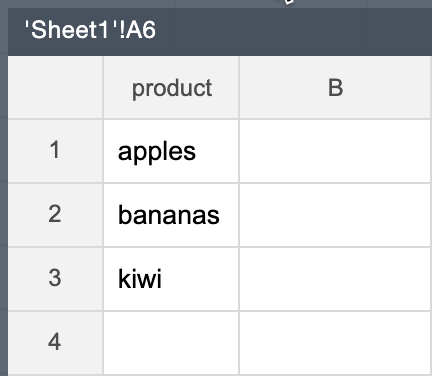
Example of an immutable operation
Now, let's perform an immutable operation over this frame by using the pipe operator "|".
In cell A7, use the following expression to add to the frame a column "quantity" and a column "price" with random numbers.
Note that as a result of this operation, the frame in cell A6 stays the same, and a new frame is created in cell A7:
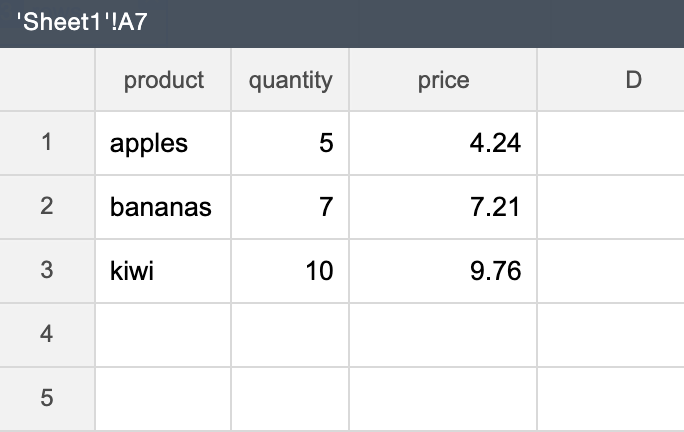
The operation doesn't change (or mutate) the original frame in cell A6 and instead creates a new frame in cell A7.
Example of a mutable operation
Ok, now let's perform a mutable operation over the same frame.
In cell A8, use the following formula to delete a row with the "kiwi" value from the target frame:
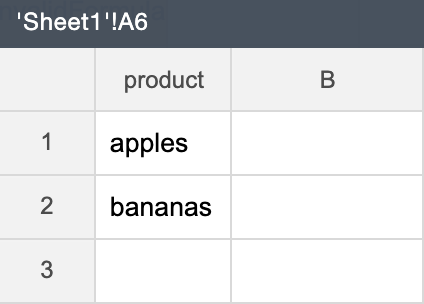
When run, the DELETE_ROW() formula doesn't create a new frame in cell A8 but modifies the existing frame in cell A6.
As a result, the frame in cell A6 gets changed:
Choosing between mutable and immutable operations
In general, it's a good idea to use immutable operations where feasible. Immutable operations only change their input frames and don't affect other frames used in your application.
Sometimes, however, you can't do without a mutable approach.